I. Pendahuluan
Metode Monte Carlo merupakan satu metode yang cukup terkenal di dalam manajemen risiko.
Manajemen risiko adalah suatu konsep dan praktek yang penting dalam dunia bisnis dan investasi.
Saat melakukan aktivitas bisnis, perusahaan atau investor seringkali menghadapi risiko yang dapat memengaruhi kinerja dan hasil akhir dari aktivitas tersebut.
Oleh karena itu, manajemen risiko sangat penting untuk meminimalkan risiko dan memaksimalkan hasil yang diinginkan.
Salah satu metode yang dapat digunakan dalam manajemen risiko adalah Metode Monte Carlo.
Metode ini merupakan teknik simulasi yang digunakan untuk memprediksi hasil dari suatu sistem atau model dengan menggunakan nilai acak atau variabel probabilitas.
Metode Monte Carlo dapat membantu perusahaan atau investor dalam memperkirakan risiko yang mungkin terjadi dalam suatu proyek atau investasi.
Dalam artikel ini, akan dibahas secara lengkap tentang Metode Monte Carlo dan penerapannya dalam manajemen risiko.
Artikel ini akan membahas pengertian Metode Monte Carlo, langkah-langkah dalam penggunaannya, keuntungan dan kelemahan dari Metode Monte Carlo, serta contoh penerapannya dalam bisnis dan investasi.
Tujuan dari artikel ini adalah memberikan pemahaman yang lebih baik tentang Metode Monte Carlo dan bagaimana teknik ini dapat digunakan dalam manajemen risiko untuk meminimalkan risiko dan memaksimalkan hasil yang diinginkan.

II. Pengertian Metode Monte Carlo
Metode Monte Carlo adalah teknik simulasi yang digunakan untuk memprediksi hasil dari suatu sistem atau model dengan menggunakan nilai acak atau variabel probabilitas.
Metode ini bekerja dengan mengambil sampel dari distribusi kemungkinan setiap variabel dalam model dan menggunakan sampel-sampel ini untuk menghasilkan hasil yang mungkin terjadi dalam suatu sistem atau model.
Metode Monte Carlo biasanya digunakan dalam situasi di mana model matematika dari suatu sistem terlalu kompleks untuk dipecahkan dengan metode matematika tradisional.
Metode Monte Carlo juga sering digunakan dalam manajemen risiko untuk memperkirakan hasil dari suatu investasi atau proyek yang mengandung ketidakpastian.
Sejarah Dan Asal Usul Metode Monte Carlo
Metode Monte Carlo pertama kali dikembangkan selama Perang Dunia II untuk membantu memecahkan masalah fisika nuklir yang kompleks.
Nama "Monte Carlo" sendiri berasal dari nama kota kecil di Monaco yang terkenal dengan kasino dan perjudian, dan dipilih oleh para ilmuwan karena metode ini menggunakan konsep probabilitas yang serupa dengan perjudian.
Metode Monte Carlo pertama kali digunakan pada tahun 1940-an oleh fisikawan Amerika Serikat bernama John von Neumann dan Stanislaw Ulam untuk memecahkan masalah yang berkaitan dengan algoritma untuk memimpin jalannya sebuah reaksi nuklir dalam sebuah sistem kompleks.
Pada saat itu, solusi matematis untuk masalah tersebut sangat sulit dihitung dengan menggunakan metode tradisional.
Oleh karena itu, von Neumann dan Ulam memutuskan untuk menggunakan nilai acak atau variabel probabilitas untuk mensimulasikan sistem tersebut, dan akhirnya menemukan hasil yang akurat melalui pengulangan metode tersebut.
Setelah itu, metode Monte Carlo mulai digunakan dalam berbagai bidang seperti fisika, matematika, dan teknik.
Pada tahun 1950-an, metode ini mulai digunakan dalam riset medis dan industri kimia, serta dalam pembangunan senjata nuklir.
Kemudian, metode Monte Carlo mulai digunakan dalam berbagai bidang lain seperti keuangan, teknik sipil, dan manajemen risiko.
Sekarang, metode Monte Carlo telah menjadi salah satu teknik simulasi yang paling penting dan umum digunakan dalam berbagai bidang, terutama dalam manajemen risiko.
Metode ini terus dikembangkan dan diaplikasikan dalam berbagai aplikasi, dan telah menjadi bagian penting dari analisis dan pengambilan keputusan yang dilakukan di banyak perusahaan dan institusi.
Prinsip Dasar Metode Monte Carlo
Prinsip dasar dari metode Monte Carlo adalah menggunakan nilai acak atau variabel probabilitas untuk mensimulasikan suatu sistem atau model.
Prinsip ini didasarkan pada asumsi bahwa jika kita dapat menghasilkan banyak nilai acak yang cukup banyak, maka distribusi hasil yang dihasilkan dari nilai-nilai tersebut akan mencerminkan distribusi yang sebenarnya dari sistem atau model yang sedang kita analisis.
Dengan kata lain, semakin banyak nilai acak yang dihasilkan, semakin akurat hasil yang kita dapatkan.
Cara kerja metode Monte Carlo adalah dengan mengambil sampel nilai acak dari setiap variabel dalam model, dan menghitung nilai hasil yang diinginkan berdasarkan nilai acak tersebut.
Sampel-sampel nilai acak ini diambil dari distribusi probabilitas yang telah ditentukan sebelumnya, seperti distribusi normal, distribusi lognormal, atau distribusi eksponensial.
Proses ini dilakukan secara berulang-ulang hingga diperoleh sejumlah besar nilai hasil yang diinginkan.
Setelah mengumpulkan sejumlah besar nilai hasil, nilai-nilai tersebut kemudian dihitung rata-ratanya untuk memperkirakan nilai hasil yang diharapkan, serta untuk menghitung variansi risiko dari hasil tersebut.
Semakin banyak nilai acak yang dihasilkan, semakin akurat perkiraan hasil yang diperoleh dan semakin akurat risiko yang terkait dengan hasil tersebut.
Dalam manajemen risiko, metode Monte Carlo digunakan untuk memperkirakan kemungkinan hasil yang mungkin terjadi dalam suatu proyek atau investasi.
Dengan menggunakan teknik ini, kita dapat memperkirakan seberapa besar keuntungan atau kerugian yang mungkin terjadi, serta seberapa besar risiko yang terkait dengan investasi tersebut.
Metode Monte Carlo sangat berguna dalam mengambil keputusan yang berhubungan dengan risiko, karena memberikan informasi yang akurat dan terukur mengenai kemungkinan hasil yang mungkin terjadi.
Langkah-Langkah Dalam Menerapkan Metode Monte Carlo
Metode Monte Carlo adalah sebuah teknik simulasi yang digunakan untuk memperkirakan kemungkinan hasil dari suatu proses yang kompleks, seperti dalam manajemen risiko.
Berikut ini adalah langkah-langkah dalam metode Monte Carlo:
- Menentukan variabel input: Pertama, kita harus menentukan variabel input yang akan digunakan dalam simulasi. Variabel input ini mungkin terdiri dari berbagai jenis data, misalnya seperti harga saham, waktu, suhu, dan lain sebagainya.
- Menentukan distribusi probabilitas: Setelah variabel input ditentukan, kita perlu menentukan distribusi probabilitas untuk masing-masing variabel input. Distribusi probabilitas ini bisa berupa distribusi normal, distribusi lognormal, distribusi eksponensial, dan lain sebagainya.
- Menghasilkan nilai acak: Selanjutnya, kita harus menghasilkan sejumlah nilai acak untuk setiap variabel input berdasarkan distribusi probabilitas yang telah ditentukan. Nilai acak ini akan menjadi input untuk proses simulasi.
- Menjalankan simulasi: Dalam proses simulasi, nilai acak yang dihasilkan akan dimasukkan ke dalam model atau sistem yang sedang dianalisis. Proses simulasi kemudian akan diulang-ulang sebanyak mungkin untuk menghasilkan sejumlah besar data hasil.
- Menghitung hasil: Setelah data hasil telah terkumpul, kita dapat menghitung statistik seperti mean, standar deviasi, atau persentasi dari data hasil tersebut. Statistik ini digunakan untuk memperkirakan hasil yang mungkin terjadi dan untuk menghitung risiko terkait dengan hasil tersebut.
- Menganalisis hasil: Setelah hasil telah dikumpulkan dan dihitung, kita dapat menganalisis hasil tersebut untuk menentukan risiko dan peluang dari suatu keputusan yang akan diambil. Analisis ini membantu dalam mengambil keputusan yang lebih baik dan berdasarkan data yang lebih akurat.
Kelebihan dan Kekurangan Metode Monte Carlo
Metode Monte Carlo memiliki beberapa kelebihan dan kekurangan yang perlu dipertimbangkan untuk penggunaannya dalam manajemen risiko.
Berikut ini adalah penjelasan lengkap mengenai kelebihan dan kekurangan metode Monte Carlo:
Kelebihan:
- Akurasi: Metode Monte Carlo sangat akurat dalam memperkirakan hasil dari suatu proses yang kompleks. Dengan menghasilkan banyak data hasil melalui simulasi, kita dapat memperkirakan peluang hasil yang mungkin terjadi dengan tingkat akurasi yang tinggi.
- Fleksibilitas: Metode Monte Carlo sangat fleksibel dan dapat digunakan dalam berbagai jenis analisis dan simulasi. Teknik ini dapat digunakan dalam manajemen risiko, analisis keuangan, optimisasi, dan berbagai jenis simulasi lainnya.
- Mengurangi ketidakpastian: Dalam manajemen risiko, ketidakpastian adalah masalah besar yang sering dihadapi oleh pengambil keputusan. Metode Monte Carlo dapat membantu mengurangi ketidakpastian ini dengan memberikan informasi yang lebih akurat mengenai peluang hasil yang mungkin terjadi.
- Memperhitungkan interaksi antar variabel: Metode Monte Carlo dapat memperhitungkan interaksi antar variabel input. Dengan menghasilkan banyak data hasil, kita dapat melihat bagaimana interaksi antar variabel dapat mempengaruhi hasil akhir.
Kekurangan:
- Waktu dan biaya: Metode Monte Carlo membutuhkan waktu dan biaya yang cukup besar dalam proses simulasi dan pengolahan data hasil. Pengolahan data yang cukup besar juga membutuhkan perangkat lunak dan perangkat keras yang memadai.
- Ketergantungan pada input yang tepat: Hasil dari metode Monte Carlo sangat tergantung pada input yang digunakan. Jika input yang digunakan tidak tepat, maka hasil yang diperoleh juga tidak akurat.
- Kesulitan dalam pemodelan: Proses simulasi yang kompleks dalam metode Monte Carlo juga membutuhkan pemodelan yang tepat dan akurat. Kesalahan dalam pemodelan dapat mempengaruhi hasil yang diperoleh dan membuat hasil menjadi tidak akurat.
- Keterbatasan dalam menghasilkan hasil yang mungkin terjadi: Meskipun metode Monte Carlo dapat menghasilkan banyak data hasil, tetapi ada kemungkinan bahwa hasil yang mungkin terjadi tidak terwakili dalam data hasil yang dihasilkan. Oleh karena itu, kita harus memperhatikan batasan-batasan dalam menghasilkan data hasil untuk mencegah kesalahan interpretasi.
Dalam keseluruhan, meskipun metode Monte Carlo memiliki kelemahan, namun kelebihan-kelebihannya cukup besar dalam membantu pengambil keputusan dalam manajemen risiko.
Oleh karena itu, metode Monte Carlo dapat menjadi salah satu pilihan yang baik dalam analisis dan simulasi dalam manajemen risiko.
III. Contoh Perhitungan Metode Monte Carlo dalam Manajemen Risiko
Metode Monte Carlo dapat digunakan dalam berbagai jenis analisis dan simulasi dalam manajemen risiko.
Untuk lebih memperjelas mengenai penerapan Metode Monte Carlo, contoh yang jelas tentu akan sangat membantu.
Oleh karena itu pada pembahasan berikut kita akan sama-sama membahas mengenai contoh perhitungan Metode Monte Carlo berdasarkan langkah-langkah yang sudah dituliskan di bagian atas tadi.
1. Menentukan Variabel Input
Pada contoh ini kita akan menggunakan sebuah permodelan proyek yang mempunyai 6 buah kegiatan (Aktifitas A, B, C, D , E,F) , berdasarkan data historis sebelumnya diketahui perkiraan jumlah biaya (dalam ribuan) seperti yang tertulis pada tabel berikut ini.

Dari variabel di atas kita bisa melihat bahwa untuk aktifitas A memiliki rentang biaya terendah Rp.4.000.000 dan tertinggi Rp.7.500.000.
Sedangkan untuk aktifitas B biaya terendahnya Rp.6.500.000 dan biaya tertingginya Rp.9.000.000.
Dan seterusnya.
Sedangkan total biaya untuk proyek tersebut terendah Rp.34.700.000 sedangkan tertingginya adalah Rp.47.700.000.
2. Menentukan Distribusi Probabilitas
Setelah kita mendapatkan variabel input, maka langkah selanjutnya adalah menentukan distribusinya.
Dalam menganalisa data ada 3 model distribusi yang biasa dikenal yaitu :
- Distribusi Normal, sering juga disebut distribusi Gaussian, adalah distribusi probabilitas kontinu yang umum digunakan dalam statistik, yang memodelkan berbagai jenis data yang terdistribusi secara simetris di sekitar nilai tengah dengan variasi tertentu. Distribusi normal memiliki bentuk seperti lonceng atau bell curve, dengan puncak yang terletak di nilai tengah dan standar deviasi yang mengendalikan seberapa jauh data tersebar dari nilai tengah.
- Distribusi Lognormal, adalah jenis distribusi probabilitas yang umum digunakan untuk menggambarkan data yang memiliki nilai minimum nol dan tidak simetris. Distribusi lognormal biasanya digunakan untuk menggambarkan data yang berkaitan dengan pertumbuhan atau perkembangan, seperti pendapatan atau harga saham. Distribusi lognormal memiliki parameter rata-rata logaritmik dan simpangan baku logaritmik yang digunakan untuk menggambarkan bentuk kurva distribusi.
- Distribusi Eksponensial, adalah jenis distribusi probabilitas yang umum digunakan untuk menggambarkan waktu antara dua kejadian yang terjadi secara acak dan independen. Contoh data yang dapat dijelaskan dengan distribusi eksponensial adalah waktu antara kedatangan pelanggan di sebuah toko. Distribusi eksponensial memiliki parameter tingkat kejadian yang digunakan untuk menggambarkan bentuk kurva distribusi.
Pada perhitungan biasanya distribusi yang sering dipakai adalah distribusi normal, karena banyak kejadian alam dan sosial yang mengikuti model distribusi ini.
Oleh karena itu dalam contoh perhitungan kali ini pun kita akan memakai model distribusi normal.
3. Menghasilkan Nilai Acak
Untuk langkah selanjutnya kita harus mulai menghitung nilai acak dari rentang variabel input yang kita punya tadi.
Misalnya untuk aktifitas A yang memiliki rentang antara Rp.4.000.000 sampai Rp.7.500.000 ditentukan probabilitas secara acak, misalnya Rp.5.750.000.
Untuk lebih mempermudah proses penentuan nilai acak kita bisa menggunakan bantuan software spreadsheet , misalnya Microsoft Excel.
Formula Excel untuk menentukan nilai acak bisa menggunakan formula sebagai berikut :
RAND()*(Biaya Maksimum-Biaya Minimum)+Biaya Minimum
Rumus ini akan menghasilkan nilai yang benar-benar acak di rentang yang telah kita tentukan.
Jadi apabila kita hitung saat ini, kemudian beberapa detik kita hitung lagi maka hasilnya pasti akan bebeda, karena nilai ini adalah nilai acak.
Dalam perhitungan yang saya coba saya mendapatkan hasil sebagai berikut :
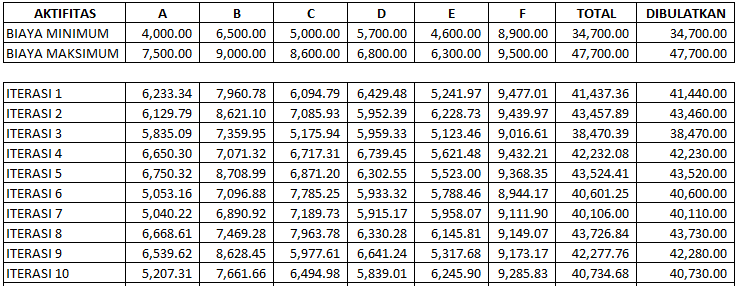
Disini saya melakukan 10 kali iterasi dengan hasil nilai acak untuk setiap kegiatan bisa dilihat pada tabel di atas.
Iterasi adalah suatu proses dimana suatu tindakan atau operasi diulang sebanyak beberapa kali, baik secara manual maupun dengan menggunakan program komputer, hingga memenuhi kondisi yang diinginkan atau mencapai tujuan tertentu.
Untuk mendapatkan hasil pada kolom DIBULATKAN anda dapat menggunakan rumus Excel :
=ROUND(_kolom TOTAL_)
Untuk kolom TOTAL sendiri diisi dengan cell pada Excel anda.
4. Menjalankan Simulasi
Mungkin sampai pada tahap ini ada yang bertanya berapa Iterasi yang harus kita lakukan untuk dapat memperoleh data yang akurat.
Untuk itu sebelum menjalankan simulasi kita harus menentukan dulu jumlah iterasi yang diperlukan agar perhitungan dan analisa Monte Carlo kita akurat.
Untuk dapat menentukannya kita bisa menggunakan Formula sebagai berikut :
ℇ = 3σ/√N
ℇ adalah nilai kesalahan
σ adalah standar deviasi
N adalah jumlah iterasi
Jadi sebelum kita mengetahui berapa banyak jumlah iterasi (N) yang kita perlukan maka kita harus lebih dahulu menentukan Nilai Kesalahan (ℇ) dan Standar Deviasinya (σ).
Rumus untuk menghitung Standar Deviasi sendiri adalah sebagai berikut :
σ = √(∑(x−x̄)2 /n)
σ adalah standar deviasi
∑ artinya penjumlahan
x̄ artinya nilai rata-rata dari seluruh data (lihat contoh perhitungan di bawah)
(x−x̄)2 adalah selisih antara variabel input dengan nilai rata-rata dipangkatkan dua (lihat perhitungan di bawah).
n adalah jumlah variabel input
Contoh Perhitungan
Berdasarkan tabel data yang kita punya di atas, maka kita punya 2 data yaitu :
- Total biaya minimum Rp.34.700
- Total biaya maksimum Rp.47.700
Berdasarkan data tersebut bisa kita ketahui :
n = 2
x̄ = (Rp.34.700 + Rp.47.700)/2 = Rp.41.200
∑(x−x̄)2 = [(Rp.41.200 - Rp.34.700) + (47.700 - 41.200)]2 -- Note : kita menghitung selisihnya
= [Rp.6.500 + Rp.6.500]2
= Rp.169.000.000
Maka berdasarkan rumus standar deviasi tadi bisa kita hitung sebagai berikut :
σ = √(169.000.000/2)
σ = √84.500.000
σ = 9192,38
Setelah menemukan nilai standar deviasi maka nilai terakhir yang harus kita temukan adalah nilai kesalahan (ℇ), rumusnya adalah sebagai berikut :
ℇ = x̄ : [1/margin]
kita misalkan kita hanya memberikan margin 2% , ini artinya bahwa metode perhitungan kita harus 98% mendekati akurat.
Maka akan kita dapat nilai kesalahan adalah :
ℇ = (34,700+47.700)/2
[1/0.02]
ℇ = 41.200/50
ℇ = 824
Sekarang setelah kita menemukan nilai standar deviasi dan nilai kesalahannya kita bisa menggunakan rumus monte carlo tadi untuk mencari nilai iterasinya.
Jika kita ingat rumus diatas tadi adalah :
ℇ = 3σ
√N
nilai ℇ sudah kita temukan adalah 824
nilai σ sudah kita temukan adalah 9192.38
maka berdasarkan formula tersebut nilainya menjadi sebagai berikut :
824 = (3 x 9192.38) = 27.577,14
√N √N
Rumus tersebut bisa kita tuliskan sebagai berikut :
N = (27.577,14/824)2
N = 1.120,06
jadi untuk mendapatkan data yang akurat dengan margin kesalahan 2% maka diperlukan 1.120 iterasi.
Dengan melakukan simulasi sebanyak 1.120 iterasi maka saya mendapatkan hasil sebagai berikut :
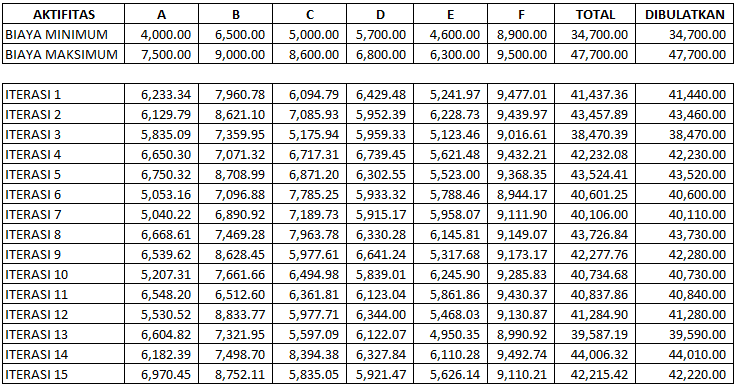
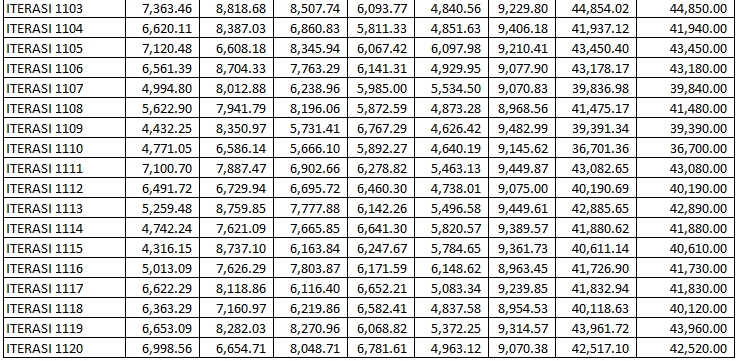
5. Menghitung Hasil
Setelah kita melakukan simulasi sesuai dengan yang diinginkan, maka selanjutnya kita akan mulai menghitung hasil-hasil yang muncul.
Disini kita akan banyak menggunakan rumus Excel untuk membantu kita menghitung hasil yang sudah kita dapatkan sebelumnya.
- Yang pertama kita akan analisa dari Tabel Excel tadi pada kolom DIBULATKAN berapa perkiraan biaya terendah dan biaya tertinggi dari proyek tersebut.Caranya blok semua data yang ada di kolom DIBULATKAN kemudian kita bisa menggunakan rumus Excel =MIN() dan =MAX()
- Berikutnya hitung nilai rata-rata dari biaya terendah dan tertinggi tersebut atau bisa juga disebut Mean dengan cara =(Biaya terendah+Biaya Tertinggi)/2
- Selanjutnya hitung standar deviasinya menggunakan rumus standar deviasi yang sudah kita pelajari di atas.
Dari data simulasi saya tadi, maka didapatkan hasilnya sebagai berikut :
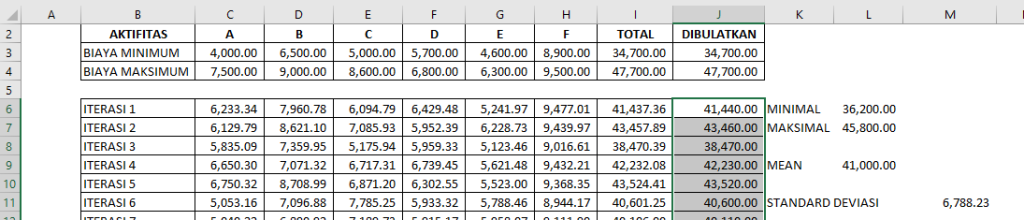
Melalui analisa ini kita sebenarnya sudah bisa sedikit mengambil kesimpulan sebagai berikut :
- Perkiraan biaya terendah dari proyek simulasi kita adalah Rp.36.200.000
- Perkiraan biaya tertinggi dari proyek simulasi kita adalah Rp.45.800.000
- Biaya rata-rata yang mungkin terjadi dari proyek ini adalah Rp.41.000.000
- Dengan kemungkinan penyimpangan Biaya Lebih (+) atau kurang (-) Rp.6.788.230
Demikian kesimpulan sementara yang bisa kita ambil, tapi proses Monte Carlo tidaklah berhenti hanya sampai disini.
Karena itu masih berupa gambaran kasar dan belum dianalisa secara lebih mendalam.
Untuk itu kita perlu melakukan analisa lebih mendalam dengan membuat distribusi frekuensi dan grafik kombinasi Probability Density Function (PDF) dan Cummulative Distribution Function (CDF) untuk melihat seberapa sering sebuah angka acak tersebut muncul.
Disini kita akan kembali menggunakan alat bantu Excel kareena data yang dianalisa cukup banyak yaitu sebanyak 1.120 angka.
Menghitung Frekuensi Data
Pertama kita copy semua angka yang ada di kolom DIBULATKAN, dengan blok semua kolom tersebut, kemudian tekan Ctrl+C.
Selanjutnya paste di sheet baru dengan menekan Ctrl+Alt+V , kemudian pilih Value (lihat gambar di bawah).
Maka semua hasil dalam kolom DIBULATKAN tadi akan ditempel dalam bentuk nilai (bukan dalam formula lagi).
Setelah kita dapat kolom dalam bentuk angka, kemudian kita akan menghilangkan semua angka yang double (berulang).
Caranya blok kolom yang baru saja anda paste tadi, kemudian klik DATA kemudian Remove Duplicates.
Maka kita akan dapat sebaran data Biaya Proyek yang akan kita analisa berapa kali Frekuensi kemunculannya dalam tabel data lengkap pertama tadi.
Berikut adalah cara menghitungnya :
- Silahkan copy data yang baru saja kita hilangkan duplikatnya tersebut ke dalam tabel analisa lengkap kita yang pertama.
- Blok tempat dimana kita akan meletakkan frekuensi kemunculan datanya, kemudian kita gunakan rumus =FREQUENCY(_data di kolom DIBULATKAN_, _data biaya yang baru saja kita copy_), setelah selesai menuliskan rumus pencet Ctrl+Alt+Enter, maka seluruh cell yang kita blok seharusnya terisi frekuensi kemunculan data biayanya.
Pada data simulasi saya hasilnya adalah sebagai berikut :

Setelah mendapatkan data frekuensi maka kita bisa membuat tabel PDF dan CDF nya sebagai berikut (sudah diurutkan dari biaya terendah ke biaya tertinggi) :
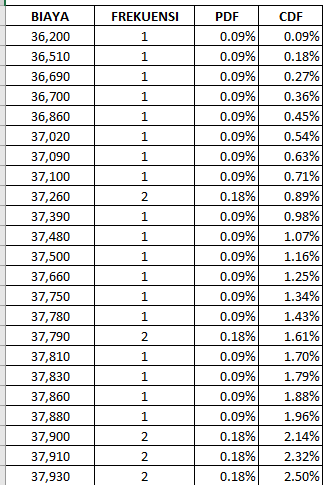
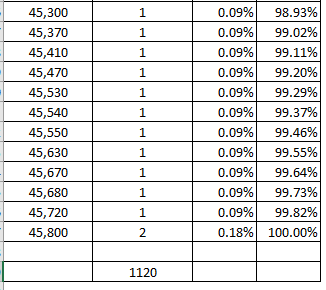
Cara menghitung nilai PDF dan CDF adalah sebagai berikut :
PDF = Nilai Frekuensi/Jumlah Data x 100%
Contoh untuk biaya 45.800 frekuensinya 2 kali.
Maka nilai PDF nya = 2/1.120 x 100% = 0,1785% dibulatkan menjadi 0,18%.
Untuk menghitung nilai CDF adalah akumulasi dari nilai PDF
CDF di baris 1 = PDF di baris 1
CDF di baris 2 = PDF di baris 1 + PDF di baris 2
CDF di baris 3 = CDF di baris 2 + PDF di baris 3
CDF di baris 4 = CDF di baris 3 + PDF di baris 4, dan seterusnya.
Setelah terbentuk tabel lengkapnya , kita kemudian bisa membuat grafik analisanya sebagai berikut :
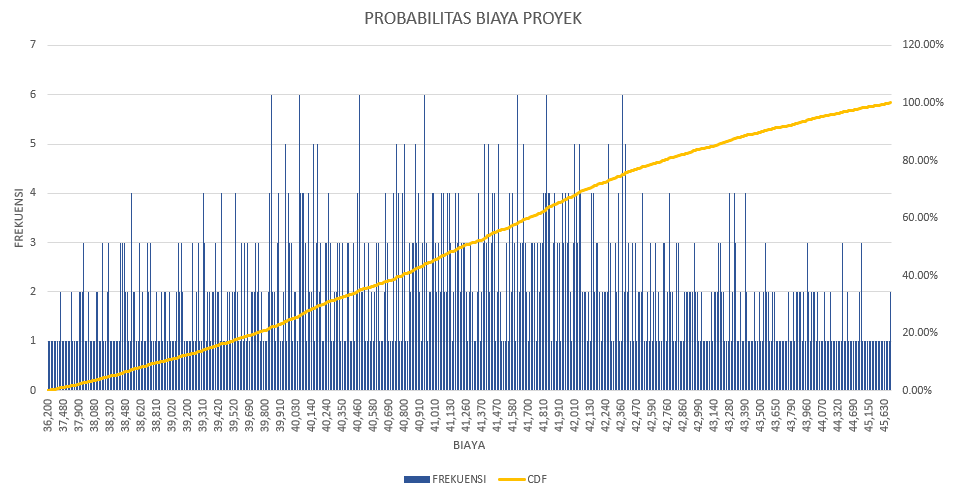
Dari tabel dan grafik tadi kita bisa dengan mudah menganalisa potensi biaya proyek yang paling sering muncul, untuk kemudian kita analisa tingkat keberhasilan dan tingkat dampak kegagalannya.
6. Menganalisa Data
Berdasarkan grafik dari langkah sebelumnya kita bisa melihat frekuensi tertinggi yang muncul adalah 6 kali, tidak ada yang lebih tinggi dari itu , maka kita akan analisa biaya-biaya yang memiliki frekuensi 6 tersebut.
Salah satunya adalah biaya Rp.40.940.000 (lihat gambar di bawah)
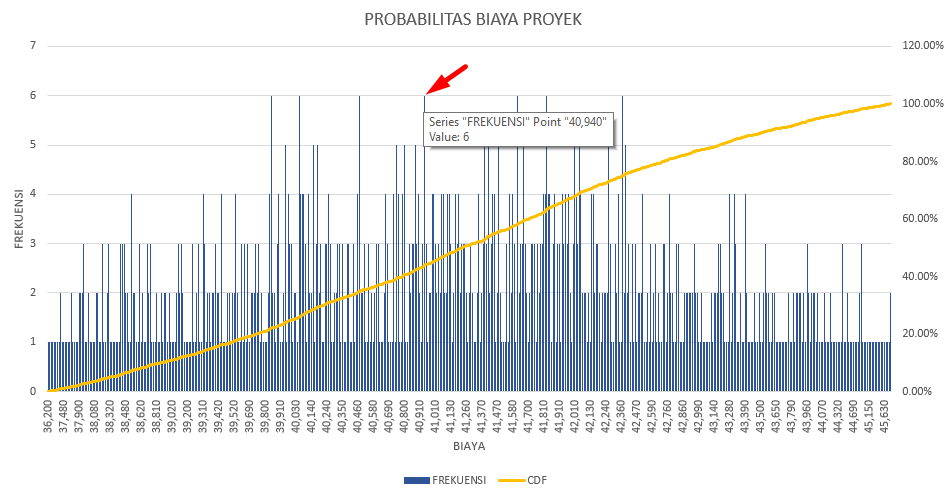
Dari grafik tersebut ada 7 biaya yang memiliki frekuensi 6 kali , oleh karena itu berdasarkan data biaya tersebut disesuaikan dengan data CDF dan PDF nya (dari tabel sebelumnya) maka bisa kita dapat tabel analisanya sebagai berikut :
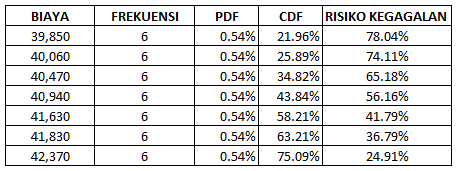
Disini bisa kita lihat jumlah-jumlah biaya proyek berdasarkan potensi keberhasilan (CDF) dan Risiko Kegagalannya (dihitung dari 100%-CDF).
Jika kita analisa maka untuk :
- Biaya Rp.39.850.000 maka tingkat kegagalannya 78.04% dan tingkat keberhasilan proyek 21,96%
- Biaya Rp.41.630.000 maka tingkat kegagalannya 41,79% dan tingkat keberhasilan proyek 58,21%
- Biaya Rp.42.370.000 maka tingkat kegagalannya 24.91% dan tingkat keberhasilan proyek 75.09%
- dsb
Jika kita lihat maka tentunya dengan biaya yang lebih tinggi maka keberhasilan proyek akan lebih besar.
Tapi semua itu tentu disesuaikan dengan kemampuan sumber daya yang dimiliki oleh perusahaan.
Dari tabel di atas maka mungkin perusahaan bisa menentukan bahwa biaya yang ideal sesuai dengan sumber daya perusahaan adalah Rp.41.630.000, dengan tingkat keberhasilan proyek 58,21% dan dampak kegagalannya 41,79%.
Berdasarkan simulasi monte carlo yang sudah kita lakukan juga kita bisa melihat, bahwa apabila perusahaan hanya memiliki kemampuan penyediaan biaya Rp.37.900.000 maka bisa dilihat bahwa tingkat keberhasilannya diperkirakan hanya 2,14 % dengan risiko kegagalan mencapai 97,86% yang tentunya sangat riskan.
Perhitungan tersebut dengan margin error sebesar 2% dan deviasi biaya +/- Rp.6.788.230
IV. Keuntungan Menggunakan Metode Monte Carlo dalam Manajemen Risiko
Selain kelebihan yang dipunyai oleh metode Monte Carlo, menerapkan metode ini pada Manajemen Risiko bisa memberikan kita beberapa keuntungan.
Pada bagian ini akan kita bahas keuntungan apa saja yang bisa kita peroleh dengan menrapkan Metode Monte Carlo pada Manajemen Risiko.
A. Keakuratan Dalam Memprediksi Risiko
Metode Monte Carlo menggunakan proses pengambilan sampel secara acak dalam simulasi.
Hal ini memungkinkan kita untuk memperkirakan distribusi probabilitas yang akurat terkait hasil yang mungkin terjadi dalam sebuah situasi tertentu.
Sehingga, metode Monte Carlo dapat memberikan perkiraan risiko yang lebih akurat daripada metode lain yang hanya berfokus pada nilai tengah atau rata-rata.
B. Mengidentifikasi Sumber Risiko
Dalam manajemen risiko, penting untuk mengidentifikasi sumber risiko.
Metode Monte Carlo dapat membantu mengidentifikasi sumber risiko dengan memperkirakan peluang hasil yang mungkin terjadi dalam situasi yang berbeda-beda.
Dengan demikian, kita dapat mengidentifikasi risiko dan memprioritaskan sumber risiko yang paling penting.
C. Mempertimbangkan Efek Interaksi Antar Risiko
Metode Monte Carlo juga memungkinkan kita untuk mempertimbangkan efek interaksi antar risiko.
Dalam situasi yang kompleks, risiko seringkali tidak terisolasi satu sama lain, melainkan saling mempengaruhi.
Metode Monte Carlo dapat memperkirakan hasil yang mungkin terjadi dalam situasi kompleks dengan mempertimbangkan interaksi antar risiko, sehingga memberikan perkiraan risiko yang lebih realistis.
D. Analisis Sensivitas dan Perubahan Variabel
Metode Monte Carlo juga memungkinkan kita untuk melakukan analisis sensitivitas dan perubahan variabel.
Dalam manajemen risiko, kita perlu mempertimbangkan kemungkinan perubahan variabel dan bagaimana hal itu dapat mempengaruhi hasil yang mungkin terjadi.
Metode Monte Carlo dapat membantu kita memahami bagaimana perubahan variabel dapat mempengaruhi hasil yang mungkin terjadi, sehingga memungkinkan kita untuk membuat keputusan yang lebih baik.
Dengan menggunakan metode Monte Carlo, pengambil keputusan dapat memperkirakan risiko dengan lebih akurat dan memprioritaskan sumber risiko yang paling penting.
Selain itu, metode Monte Carlo juga memungkinkan kita untuk mempertimbangkan interaksi antar risiko dan melakukan analisis sensitivitas dan perubahan variabel.
Dalam hal ini, metode Monte Carlo sangat berguna dalam manajemen risiko dan dapat membantu pengambil keputusan dalam membuat keputusan yang lebih bijaksana dan tepat.
V. Kesimpulan
Dalam artikel ini, kita telah membahas tentang metode Monte Carlo dan penerapannya dalam manajemen risiko dan bisnis.
Metode Monte Carlo merupakan teknik simulasi acak yang digunakan untuk memodelkan situasi atau masalah yang kompleks dengan memperhitungkan kemungkinan berbagai hasil yang mungkin terjadi.
Dalam manajemen risiko, metode ini berguna untuk memprediksi potensi kerugian atau keuntungan dan membantu pengambilan keputusan yang tepat.
Penerapan metode ini juga dapat membantu perusahaan dalam melakukan analisis sensitivitas dan perubahan variabel, sehingga dapat membuat keputusan yang lebih baik dan akurat.
Dalam kesimpulannya, metode Monte Carlo merupakan teknik yang sangat berguna dan fleksibel dalam memodelkan situasi yang kompleks dan membantu pengambilan keputusan yang tepat.
Namun, perlu diingat bahwa metode ini juga memiliki beberapa keterbatasan dan kelemahan.
Oleh karena itu, sebelum menggunakannya, kita harus memperhatikan dengan cermat asumsi dan parameter yang digunakan dalam simulasi serta mempertimbangkan faktor lain yang dapat memengaruhi hasilnya.
Demikianlah pembahasan kita, semoga artikel ini bisa berguna dan membantu setiap anda yang sedang ingin mengetahui mengenai metode Monte Carlo.
Dengan bantuan teknologi saat ini, maka pengelolaan manajemen risiko, tidak perlu lagi dilakukan secara manual sehingga membutuhkan usaha dan tenaga yang tidak sedikit.
Banyak aplikasi manajemen risiko yang sudah tersedia saat ini, salah satunya adalah aplikasi ERMS dari Riskindo yang merupakan aplikasi terlengkap dan mudah digunakan.

Referensi : Simulasi Monte Carlo Dalam estimasi Biaya Proyek

